👀 목차
- 알고리즘 기초를 이해한다.
- 이진 탐색 알고리즘을 작성한다.
- 알고리즘 실행 시간을 알려주는 빅오 표기법에 대해서 배운다.
- 가장 느린 알고리즘인 외판원 문제를 살펴보자.
1. 들어가는 글
알고리즘에서 배울 것
- 여러 가지 알고리즘들의 차이점을 이해해야한다. 이해하지 못한다면, 미리 구현한 알고리즘은 필요가 없습니다.
- 여러 가지 알고리즘 장단점을 배우게 된다. 이때 단순히 다른 자료구조를 사용하는 것만으로도 성능이 크게 달라질 수 있다.
2. 이진 탐색
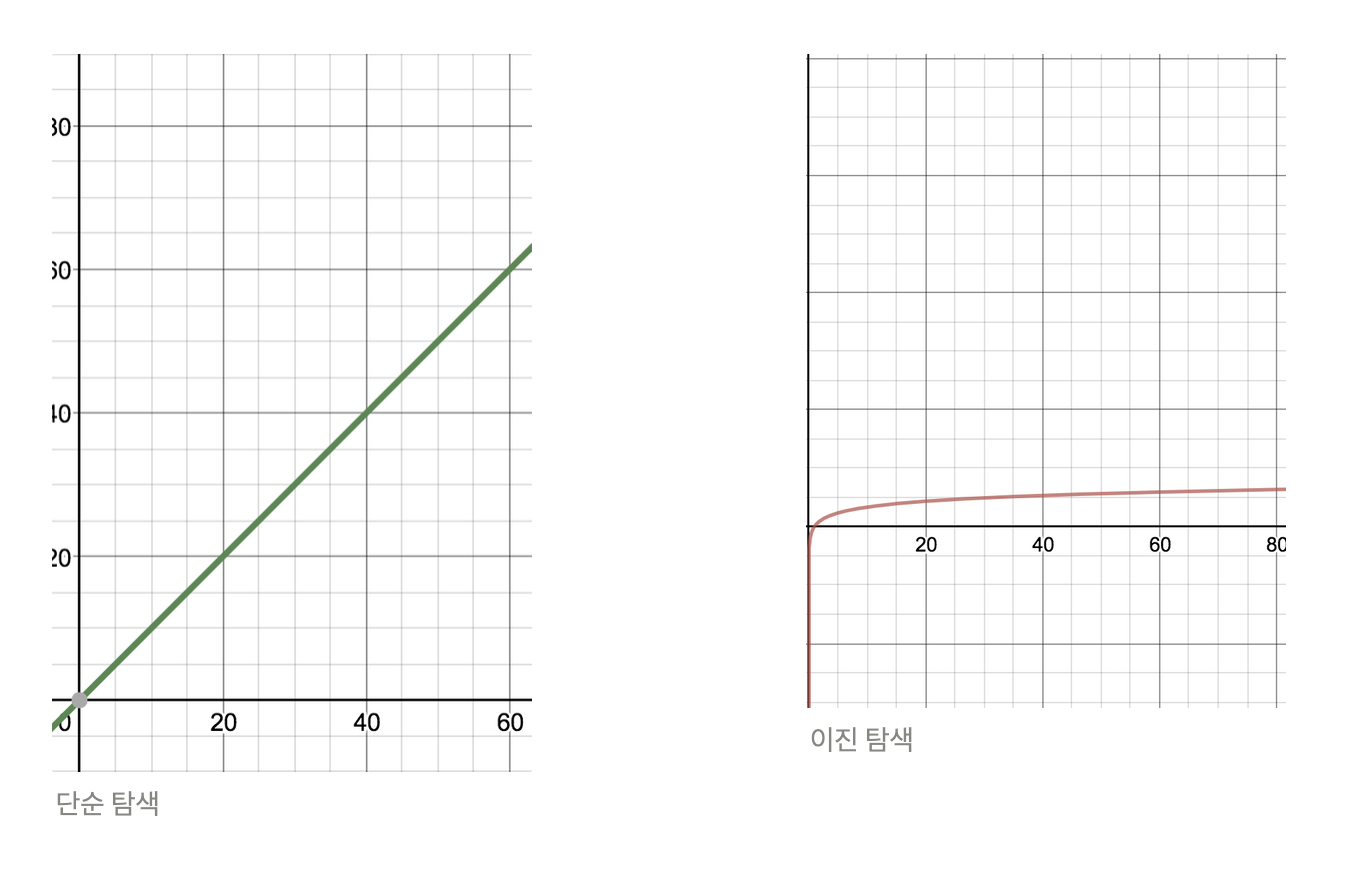
- 단순 탐색 vs 이진 탐색
| 단순 탐색 | 이진 탐색 | |
|---|---|---|
| 의미 | 순서대로 추측하는 것 | 중간을 탐색해서 비교해서 추측 |
| 예시 | “lena”를 전화번호에서 찾기 위해 처음부터 찾는 경우 | “lena”를 전화번호에서 찾기 위해 중간부터 찾는 경우 |
| 빅오 표기법 | O(n) | O(log n) 로그 2n |
| 참고 | 바보 탐색 | 리스트의 원소가 정렬되어 있어야한다. 예를 들면, 전화번호부 |
이진 탐색 함수 코드
def binary_search(list, item):
"""
이진 탐색 함수
:param list: 정렬된 리스트
:param item: 찾고자하는 숫자
:return: 해당 숫자 인덱스
"""
low = 0
high = len(list) - 1
while low <= high:
mid = (low + high) // 2
guess = list[mid]
if item == guess:
return mid
elif item < guess:
high = mid -1
else:
low = mid + 1
return None3. 빅오 표기법
우리는 다른 사람들이 만든 알고리즘을 사용할 것이다. 이때 어떤 알고리즘이 빠른지 알아야 하는데 이때 사용하는 것이 빅오 표기법이다.
빅오 표기법 규칙
1 . 알고리즘 속도는 시간이 아니라 연산 횟수가 어떻게 증가하는지 로 나타낸다.
- 이유? 속도로 할 경우, 이진 탐색의 경우는 리스트가 많아지면 더 속도 비율이 빨라지는데 이를 표현할 수 없다. 2 . 빅오표기법은 최악의 경우만 나타낸다.
- 단순 탐색으로 한번에 추측했어도 여전히 O(n) 이다.
빅오 표기법
O(log n) - O():큰 영어 O를 의미한다.
- n: 리스트 수
- log n 즉, ()안은 연산 횟수를 의미
많이 사용하는 빅오 실행 시간의 예
 Hello Coding 그림으로 개념을 이해하는 알고리즘 책 이미지 참고
Hello Coding 그림으로 개념을 이해하는 알고리즘 책 이미지 참고
- O(log n) : 로그 시간. 예) 이진 탐색
- O(n) : 선형 시간. 예) 단순 탐색
- O(n*log n) : 예) 퀵 정렬
- O(n^2) : 예) 선택 정렬
- O(n!) : 예) 외심원 문제 > 5개의 도시를 가장 최단 시간에 가려면?
4. 외판원 문제
설마 실행 시간이 O(n!) 는 없겠지!라고 생각할 수 있습니다. 그런데 외판원 문제는 느린 알고리즘 중 하나입니다.
외판원 문제
- 외판원 이름을 오푸스라고 하자. 오푸스는 가장 짧은 거리를 통해 다섯 개의 도시를 방문하고 싶습니다. 이 문제를 풀기 위해서는 도시를 방문하는 모든 경로를 살펴보는 것 입니다.
- 그럼 도시가 4개인 경우면 , 432*1(4!) 입니다.
- 따라서 빅오 표기법은 O(n!) 입니다.
소스 코드
참고
- Hello Coding 그림으로 개념을 이해하는 알고리즘